「優位性がある」とはどのようなものでしょうか。
この記事では、あるべきトレード手法の形について簡単に考えるために、FXの局面について考えるのではなく「サイコロの目を当てるゲーム」を例に優位性を紹介します。
例題:サイコロの目を当てるゲーム
あなたはサイコロの目を当てるゲームに参加します。
すべての目(1~6)が同様に確からしい※確率で出る六面体のサイコロをディーラー(親)が振り、出た目を当てるゲームです。
選択肢は
- A:2~6が出る
- B:1が出る
の2択で、どちらかに賭けます。
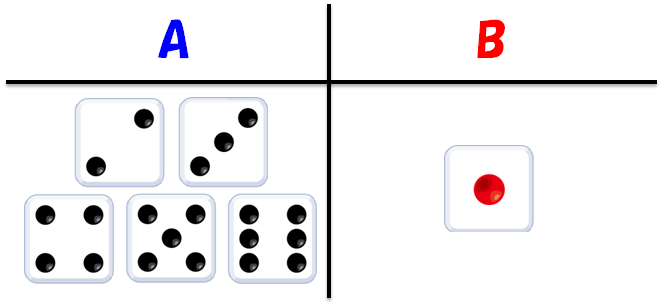
スタート時点で100P(ポイント)を所有しており、賭ける際に10Pを支払います(手数料)。
正解すると20Pもらえ(手数料を引くと+10P)、不正解だともらえません(同-10P)。
あなたはこのルールの中でどのような戦略を取りますか?
回答例
このような問いに対して出てくる回答は、概ね以下の2パターンと考えられます:
常にAに賭け続ける

サイコロを振ってAが正解になる確率は6分の5(≒83.33%)、確率が高い方に賭け続けるという方法です。
6回に5回はAに、6回に1回はBに賭ける

彼は勝率100%を狙うために、6分の1の確率で正解になるBも狙う戦略を立てました。うまくいけば勝率100%も夢ではありません。
常にAに賭け続けた場合
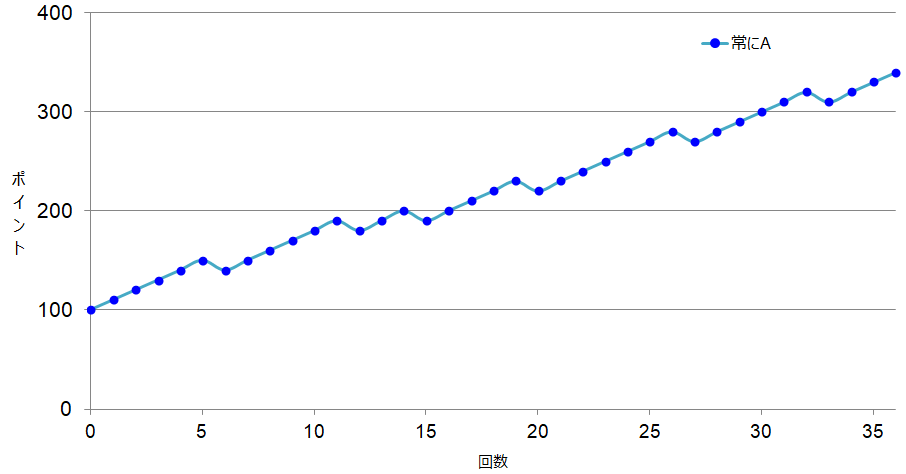
結論から言うと、この「Aに賭け続ける」戦略がこのゲームにおいて最も効率的にポイントを稼げる戦略です。
何があっても常にAに賭け続ける場合、勝つ確率は83.33%となります。
その結果、ポイントは6回賭けるごとに40Pのペースで増えることが期待できます(5勝1敗ペース…50-10=40P)。
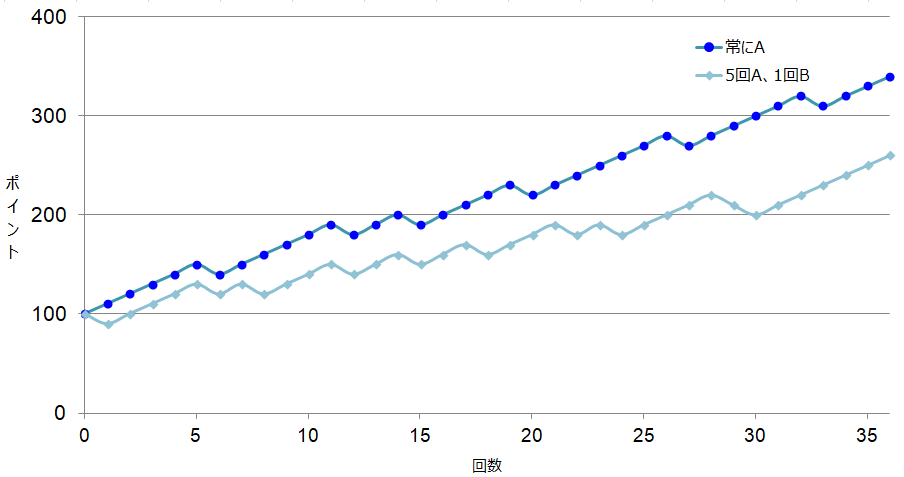
グラフで示すと、以下のような上昇のグラフが描けます:
「トレーダー的思考」…より高い期待値を求めること
6回ごとに40P増えるため、40を6で割った6.66…≒6.67がこの戦略の「期待値」となります。
期待値とは、1回賭けるごとに得られることが期待できる値のことで、期待値がプラスだとポイントは増えていく方向、マイナスだと減っていくことになります。
Aに賭け続けると期待値6.67が得られる…これ(一貫した手法を取り続けるとポイントが増えていく状態)こそが「優位性のある仕掛けパターンを有している」という状態です。
しかも「Aに賭け続ける」だけなので、実行も非常に容易です。
私は「最高効率の戦略を求めた上でその戦略をやり通す」考え方を「トレーダー的思考」と定義しています。
このトレーダー的思考こそが、FXで勝てる手法を組み立てるために必要な要素であると考えます。
6回に5回はAに、6回に1回はBに賭ける場合
一見理にかなっているように感じるこの戦略ですが、残念ながらAを賭け続ける戦略よりも勝率・期待値ともに劣ります。
結論だけ書くと、この戦略の勝率は72.22%(常にAに賭ける場合と比べると11.11%低い)で、期待値は4.44(常にAに賭ける場合と比べると2.23低い)となります。
一応期待値はプラスなので「優位性のある仕掛けパターン」ではありますが、6.67の期待値を叩き出す「Aに賭け続ける戦略」よりも低くなっています。(下図参照)
計算法(省略可)
※「答えだけでいいよ」という方は、飛ばしていただいて構いません。
- 勝率
- 83.33%の確率で起こること(サイコロを振って2~6が出る確率)を6回中5回の割合で賭けて当たる確率:5/6 × 5/6 = 25/36 ≒69.44%
16.67%の確率で起こること(サイコロを振って1が出る確率)を6回中1回の割合で賭けて当たる確率:1/6 × 1/6 = 1/36 ≒ 2.78%
よって、6回に5回はAに、6回に1回はBに賭けたときに当たる確率は69.44 + 2.78 = 72.22%
-
期待値(計算例)
- 36回ゲームを行うと、30回Aに、6回Bに賭ける計算になる。
- 30回Aに掛けた場合の確率上の稼げるポイント:200P(勝ち25回:250P、負け5回:-50P)
6回Bに掛けた場合の確率上の稼げるポイント:-40P(勝ち1回:10P、負け5回:-50P) - よって、30回Aに、6回Bに賭けた場合の確率上の稼げるポイント:200-40 = 160P
期待値(確率上のゲーム1回あたりで稼げるポイント)は160/36 ≒ 4.44
「ギャンブラー的思考」…それは戦略をより複雑にする敗者の思考
6回中5回はAになるが1回はBになる、つまり、6回中Aに5回、Bに1回のペースで賭ければ勝率100%が狙える…むしろ、そのように賭けないと100%になれない…
そもそもずっとAに賭けていたら、勝率100%になれない…トレーダーたるもの100%を狙うべき、そしてそれを手中に収めてこそ「最強のトレーダー」なのだ…
このような考えを持ったトレーダーは少なからずいらっしゃると思います。
しかし、この考えは大きな間違いです。
上記の考えはトレーダー的思考ではなく、「ギャンブラー的思考」と私は考え、定義しています。
時には確率の概念を突破し、そして確率を超える勝率(期待値)を手に入れられるかもしれません…それはとてもロマンがあります。
しかし、トレードにロマンは不要です。追い求めるべきは「期待値」であり、それに付随するのが「勝率」や「一貫性」というような概念です。
心理的な考察
「トレーダー的思考」と「ギャンブラー的思考」…この2つの思考によってもたらされる心理的な動作について考察します。
なぜ、トレードにギャンブラー的思考を持ち込むのが悪なのか…それが期待値の良し悪しだけでなく、破滅への思考であるから(経済的にも人格的にも)ということを理解していただければと思います。
主観的な意見が入っていますが、書いてある内容は大方みなさんも経験済なのではないかと思います(もちろん私はなんらかの形で何度も経験済)。
トレーダー的思考による例題の結果に対する心理的反応
トレーダー的思考では「A一択」のため、想定される結果パターンは2通りです。
A(高確率)に掛けてAが正解になった場合
期待通りの結果。なぜなら83.33%という確率上優位性が高い選択をしているのだから(冷静)。
A(高確率)に掛けてB(低確率)が正解になった場合
6分の1(16.67%)で起こることが起こってしまった。仕方がない(納得)。
以上のように「勝負の結果を確率で理解している」ため、結果に対して動揺や怒りという感情は湧きません。
賭けが外れても「仕方がない」と受け止めることができるようになり、淡々とAに賭け続けることができます。
このような心理状態が保てていることを、一般にゾーンに入っている状態と定義されています。
マーク・ダグラス氏の著書「ゾーン」もいわばこの状態をつくることを目的とした本といえます。
余談ですが…さらに上級者になると、このような考えを持つことができるかもしれません。
2回連続Bになった場合(連続不正解)
6分の1で起こることが2回連続…つまり36分の1で起こることが今起きた。めっちゃ珍しいものが見れた。2連続で外れちゃったけどなんか逆にワクワクする。次またBだと216分の1のことが起こったことになるのか。それはそれで楽しみだが次も当然Aに賭ける。
ギャンブラー的思考による例題の結果に対する心理的反応
ギャンブラー的思考では、AとB両方に賭けていたため、その結果パターンは4つになります。
A(高確率)に賭けてAが正解になった場合
期待通りの結果(冷静)。
B(低確率)に賭けてBが正解になった場合
6分の1で起こることをドンピシャで当てられて最高の気分(高揚感)。
自分は他人にはない才能があるのかもしれない(錯覚)
B(低確率)に賭けてA(高確率)が正解になった場合
仕方ない。もともと低確率(6分の1)の事象を当てようとしているのだから(「トレーダー的思考」において、高確率に賭けて低確率なことが起こったときと同様の納得)。
A(高確率)に賭けてB(低確率)が正解になった場合
この前はBに賭けて当たったのに外した(偶然)
正直そろそろBが出ると思っていた(錯覚)
自分がAに賭けた時に限ってBが出るとか腹が立つ(怒り)
どうせ次Bに賭けたらAになるんだろう(被害妄想、戦略破綻の序章)
ギャンブラー的思考はさまざまな感情を引き寄せます。
ギャンブルにハマり、依存症になって借金を抱えても辞められなくなる理由は、いつの間にか結果よりも高揚感を追い求めるようになって、期待値がマイナスの賭けをし続けるからと考えます。
このようなタイプの人は、気がついたら当初の戦略が変わってAとBの賭けるペースが同じになったり(むしろBのほうが賭ける回数が増えてくる)、Bを賭けるときにより多くの額(ポイント)を賭けるようになります(より強い高揚感を求めるため、今回のルールではできないが)。
その結果、気がついたら期待値がマイナスになるような賭けを行ってしまい、雪だるま式に負債が増えていき、いずれポイントは0になるでしょう。
感情は繰り返すごとに増幅し、いずれ爆発する
予想を外すことが増えるにつれ、上記の内容(怒りや錯覚)はさらにエスカレートしていきます。思考は繰り返せば繰り返すほどその人の中で「確信」として植え付けられるからです。
やや極端な人の例かもしれませんが、以下のようになる可能性は十分に起こり得ます:
A(高確率)に賭けてAが正解になった場合
自分がAに賭けたんだからAになるに決まっている(傲慢)
最初からずっとAであり続けろ(強欲)
B(低確率)に賭けてBが正解になった場合
当然の結果(納得、高揚感は薄れている)
自分がBに賭けたのだからBにならないとおかしい(錯覚)
B(低確率)に賭けてA(高確率)が正解になった場合
ディーラーがなんらかのイカサマをしているに違いない(疑心)
サイコロに細工がされているのではないか(疑心)
自分がBに賭けたからAになった(被害妄想)
当たるまでB(低確率)に賭けてやる(優位性の破綻)
A(高確率)に賭けてB(低確率)が正解になった場合
ディーラーは自分がAに賭けたからBになるように仕向けた(被害妄想)
ディーラーは自分が勝てないようにサイコロを振っているに違いない(被害妄想)
ディーラーがこっちを見て鼻で笑った(幻覚)
確率なんて所詮机上の空論にすぎない(数学の否定)
運命は自分の存在を否定している(自己否定)

トレードはギャンブルではありません。
そのことを納得し、ギャンブラー的思考からトレーダー的思考に転換する必要があります。
「悪しき成功体験」がもたらす悲劇
トレーダーがギャンブラー的思考に陥ってしまう要因のひとつが、「低確率で起こることを当てたとき」です。
低確率で起こることを当てだすと、あたかもその低確率な事象が数値以上に高い確率で起こりうるように錯覚してしまい、そして確率通りに起こる低確率な事象に少しずつポイント(資産)を失われていくのです。
私はこの過程の冒頭部分を「悪しき成功体験」と定義しています。
本来成功するべきでないことを成功してしまったが故に、そしてその時に得た高揚感を再度手に入れたいが故に、低確率のことを当てることに心血を注ぎ始め、「ポイントを増やす」目的で行ったはずのゲームが「低確率を当てる」ものに変わっていき、ギャンブラー的思考に陥っていく…と考えています。
サイコロの数字を予想するのに才能など必要ない
低確率の事象を当てると、極端な表現をすると「天に魅入られている」とか「自分には才能がある」と錯覚してしまいがちです(もちろんそうならない人もいます)。
しかし、たかがサイコロの数字当てゲームに才能など一切必要ありません。
必要なのは確率の計算と期待値の算出だけです。
つまり、勝負を始める前に勝負が決まっている必要があります(例題だと、「Aに賭け続ける」という戦略を確定させること)。
何事も起こりうる
Bが起こる確率(サイコロを振って1が出る確率)は6分の1(16.67%)ですが、2回連続Bになること(36分の1:2.78%)も当然起こり得ます。もちろん3回連続Bになること(216分の1:0.463%)もあり得ます。
確率統計上は極めて低い確率ですが、分子に1以上の数値がついている限りそれは起こる得るものとなります。
確率を学んでいくと1%以下のことは「実質起こらない(=0%に近似できる)」と考えてしまうかもしれませんが、そこは大きな間違いです。
「何事も起こりうる」…このことは頭の片隅に置いておく必要があります。
そして、何事も起こりうることを想定した資金管理が必要になってくる…ということもいえます(このことは資金管理の章で説明します)。
余談:いろんな確率
・6回サイコロを振って6回ともA(2~6)が正解になる確率
33.5%
→Aに賭け続けていれば、33.5%の確率で6連勝ができる
・6回サイコロを振って5回A、1回Bが正解になる確率
40.2%
→意外と低い(?)ように見えますが、1番確率が高いパターンです(2番目は全部Aが正解となる33.5%)
・6回サイコロを振って6回ともB(6)が正解になる確率
0.00214%(46656分の1)
→ほぼあり得ない(でもあり得る)
優位性がない局面とは?優位性がない場合どうするか
さきほどの例題は、思考法の違いはあれど、Aに賭け続ける、Aに5回・Bに1回のペースで賭けるという戦略のどちらにも優位性がありました。
では、今度は優位性がない場合について考えたいと思います。
サイコロの目を当てるゲームに置き換えるとかなり茶番ですが、私達はFXにおいて同じような局面でも際限なくトレードに参加し、そして資産を減らしています。
例題2)優位性がないゲーム
あなたはサイコロの目を当てるゲームに参加します。
すべての目(1~6)が同様に確からしい確率で出る六面体のサイコロをディーラー(親)が振り、出た目を当てるゲームです。
選択肢は
- A:奇数(1, 3, 5)
- B:偶数(2, 4, 6)
の2択で、どちらかに賭けます。
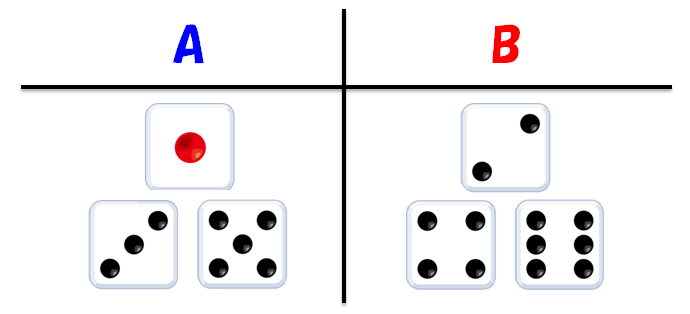
スタート時点で100P(ポイント)を所有しており、賭ける際に10Pを支払います(手数料)。
正解すると19Pもらえ(手数料を引くと+9P)、不正解だともらえません(同-10P)。
あなたはこの状況下でどのような戦略を取りますか?
回答例
選択肢が変化し、正解時にもらえるポイントが1Pだけ減りました。
A、Bどちらも確率が50%であることは容易にわかります。
この場合はどのような戦略を立てるべきでしょうか?
常にAに賭け続ける

その時の感覚でAかBのどちらかを選ぶ

ときには交互に、時には連続とかいいんじゃないでしょうか?
果たしてどちらのほうが多くポイントを稼げるでしょうか。
勝者のいない世界
結論から書くと、残念ながらこのゲームは参加すればするほどポイントが減っていく残酷なゲームです。
勝率はA一択であろうと、AB交互選択であろうと、最終的には5割に近い成績に落ち着きます(やればやるほど5割に収束する)。
しかし、「勝って+9P、負けて-10P」というルールのため、確率通り1回勝って、1回負けるごとに所有ポイントは1P減ることになります。
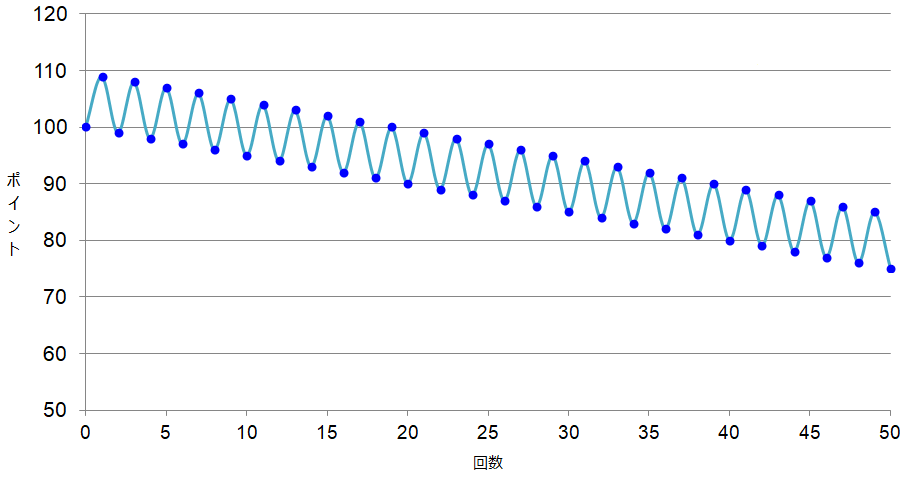
その結果、下のグラフのように、着実にポイントを減らしていく結果となってしまいます(下のグラフは美しいくらいに勝ちと負けを繰り返した場合における、ポイントの変化を示している):
2つの戦略の期待値は、両方とも-0.5とマイナスです(1回賭けるごとに平均して0.5P失ってしまう)。
このように、期待値がマイナスになる場合を「優位性がない」といいます。
「何もしないこと」が勝者になるゲームがここにある
では、このゲームの戦略の最適解は…
そう、「ゲームに参加せず、何もしない」となります。
ゲームに参加する度にポイントが失われるような勝負は参加しなければ良い…この考えはサイコロの目を当てるゲームだけでなく、FXにおいても非常に重要な考えです。
トレードに立ち返る
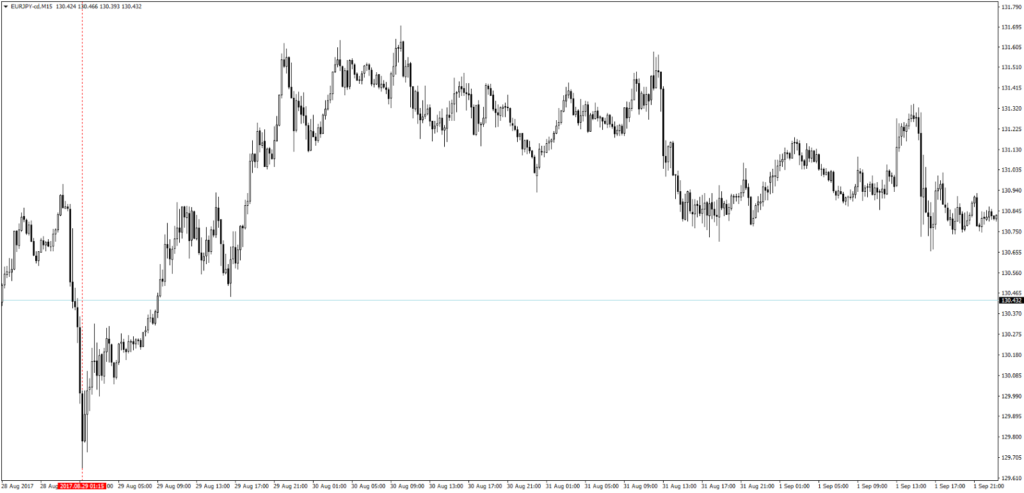
賭ければ賭けるほど負ける、このような場面はFXにはかなりの割合において存在します。
というのも、ある局面で5pipsの利益を得ようとしたとき、買っても売っても50%の確率で目標に到達するからです。
マーケットの値動きの大半(約9割…とも言われているが明確な数値はない)は、50%の確率で上昇し、50%の確率で下落する「ランダムウォーク」の相場です。この相場の中でトレードを仕掛けることは、先程の「やればやるほどポイント(=資産)が減る」悪夢の仕掛けといえます。
「勝率が5割ならば、資金は増えもせず減りもしないのではないか」と思うかも知れません。
しかし、FXには「スプレッド」という要素があります。
仕掛けから+5pips動いても、スプレッド分を考慮すると+4.5pipsであったり+4pipsとなります。一方-5pipsの損失は-5pipsです。
このスプレッドの存在が、仕掛ければ仕掛けるほど負けてしまう例題2の、勝ち分の負け分の差に相当します。
優位性のない局面で仕掛けるのは無駄な行為です。優位性のある局面でのみ仕掛けることが重要ということが分かります。
その優位性のある局面を見つける方法(ランダムウォークでない約1割ほどの優位性のある局面を見つける方法)として、当サイトではプライスアクションを利用する…ということです。

注意:「ランダムウォーク」は数pipsレベルの範囲(もっと厳密にいえばティックレベル)での話であることに気をつけましょう。仕掛けから100pips離れたところに指値と逆指値をつけた場合も勝率は5分5分…というのは間違いです(もしこれが事実ならFXで勝つことは理論上不可能で、FXは「ギャンブルマシン」と化す)。
まとめ
- 優位性があるとは、「期待値がプラス」であるということ。「期待値がプラス」とは、狭義では「1回の仕掛け(トレード)がもたらす利益の平均値」のこと、広義では「長期的に見て資産を増やせるという確信がある」ということ。
- 「優位性のある仕掛けが実行できる」条件は、「Aを選択し続ける」のように容易で複雑さがないということ。FXにおける仕掛けタイミングもそれくらい容易であることが望ましい。
- 優位性がないとは、「期待値がマイナスである」ということ。優位性のない局面で仕掛ければ仕掛けるほど資産は減っていくため、仕掛けないことが重要。
- 優位性のない場面で仕掛けないようにする方法は、「優位性がある」と判断できる局面以外で仕掛けないこと(「ただなんとなく」で仕掛けないこと)。






コメント